Which Regression Equation Finest Suits the Information units the stage for this enthralling narrative, providing readers a glimpse right into a story that’s wealthy intimately and brimming with originality from the outset. Regression evaluation is a strong instrument used to determine the connection between variables, and deciding on the right regression equation is essential in acquiring correct outcomes. From linear to polynomial, logarithmic to non-linear, this complete information will cowl the assorted forms of regression equations and supply a transparent understanding of how one can choose one of the best one for a given dataset.
The significance of choosing the right regression equation can’t be overstated. A poor alternative can result in inaccurate predictions and flawed conclusions. Subsequently, it’s important to know the various kinds of regression equations and how one can apply them to real-world datasets. On this narrative, we are going to delve into the world of regression equations, exploring the completely different strategies for becoming knowledge, evaluating the match of a regression equation, and figuring out one of the best regression equation for a given dataset.
Definition of Regression Equation

Regression equations are statistical fashions used to research the connection between a dependent variable and a number of impartial variables. They’re broadly utilized in numerous fields, together with economics, finance, social sciences, and engineering. The first aim of a regression equation is to determine the connection between variables and make predictions or forecasts.
Totally different Forms of Regression Equations
There are a number of forms of regression equations, every with its personal common kind and utility. Understanding the traits of every kind is essential for choosing essentially the most acceptable mannequin for a given dataset.
Forms of Regression Equations
- Easy Linear Regression:
- A number of Linear Regression:
- Polynomial Regression:
- Logarithmic Regression:
- Shrinkage: Lasso regression shrinks the coefficients of the variables, making them extra secure and fewer vulnerable to overfitting.
- Subset choice: By forcing sure coefficients to turn into zero, Lasso regression selects a subset of essentially the most related options for the mannequin.
- Stability: Lasso regression tends to supply extra secure fashions, making it simpler to estimate the affect of every variable.
- Shrinkage: Ridge regression shrinks all of the coefficients in the direction of zero, making them extra secure and fewer vulnerable to overfitting.
- Stability: Ridge regression produces extra secure fashions, making it simpler to estimate the affect of every variable.
- No subset choice: Not like Lasso regression, Ridge regression doesn’t choose a subset of essentially the most related options for the mannequin.
- Logistic regression: That is used for binary classification issues, the place the hyperlink operate is the logit operate.
- Generalized additive fashions (GAMs): These fashions permit for non-linear relationships between variables, making them a preferred alternative for complicated knowledge units.
- Poisson regression: That is used for depend knowledge, the place the hyperlink operate is the log operate.
- Listwise deletion: That is essentially the most simple methodology, the place observations with lacking values are merely faraway from the evaluation.
- Imputation: This entails filling within the lacking values with a predicted worth, often based mostly on the means or medians of the opposite variables.
- A number of imputation: This entails creating a number of copies of the information set, every with a special set of imputed values.
Easy linear regression is a regression mannequin with one impartial variable. It’s the easiest type of regression and is used when there’s a linear relationship between the variables. The overall type of a easy linear regression equation is:
/blockquote> Y = β0 + β1X + ε
The place:
– Y is the dependent variable
– β0 is the intercept or fixed time period
– β1 is the slope coefficient
– X is the impartial variable
– ε is the error time period
A number of linear regression is an extension of straightforward linear regression with a number of impartial variables. The overall type of a a number of linear regression equation is:
/blockquote> Y = β0 + β1X1 + β2X2 + … + βnXn + ε
The place:
– Y is the dependent variable
– β0 is the intercept or fixed time period
– β1, β2, …, βn are the slope coefficients
– X1, X2, …, Xn are the impartial variables
– ε is the error time period
Polynomial regression is a sort of regression mannequin the place the connection between the variables is non-linear. The overall type of a polynomial regression equation is:
/blockquote> Y = β0 + β1X + β2X^2 + … + βnX^n + ε
The place:
– Y is the dependent variable
– β0 is the intercept or fixed time period
– β1, β2, …, βn are the coefficients
– X is the impartial variable
– ε is the error time period
– n is the diploma of the polynomial
(Logarithmic regression) a selected case of polynomial regression within the case of exponent as 1, is used when the connection between the variables is logarithmic in nature. The overall type of a logarithmic regression equation is:
[blockquote> Y = β0 + β1ln(X) + ε
The place:
– Y is the dependent variable
– β0 is the intercept or fixed time period
– β1 is the slope coefficient
– X is the impartial variable
– ε is the error time period
– ln represents the pure logarithm
Significance of Choosing the Appropriate Sort of Regression Equation, Which regression equation most closely fits the information
Choosing the right kind of regression equation is essential for correct predictions and evaluation. The kind of regression equation will depend on the character of the dataset and the analysis query. Utilizing the unsuitable kind of regression equation can result in inaccurate outcomes and incorrect conclusions. It is important to evaluate the connection between the variables and select a regression equation that precisely represents the information.
Idea of Residuals in Regression Evaluation
Residuals are the variations between the noticed values and the anticipated values in a regression evaluation. They’re a vital part of regression evaluation and are used to judge the efficiency of the regression equation. The residuals must be randomly scattered across the horizontal axis, indicating that the regression equation is an efficient match for the information.
Interpretation of Residuals
Residuals might be interpreted in a number of methods:
– Residuals near zero point out that the regression equation is an efficient match for the information.
– Residuals which are persistently optimistic or destructive point out a non-linear relationship between the variables.
– Massive residuals point out that the regression equation just isn’t a great match for the information.
Superior Subjects in Regression Equations
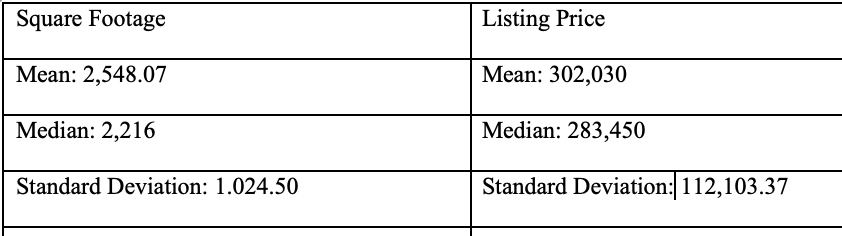
Within the realm of regression evaluation, the pursuit of accuracy and precision is unending. Because the complexity of the information grows, so do the challenges in figuring out the best mannequin. Superior subjects in regression equations present a set of strategies to deal with these challenges, making certain that the fashions we construct are each dependable and significant. This contains using regularization strategies, generalized linear fashions, and progressive strategies for dealing with lacking knowledge.
Regularization Strategies: Stopping Overfitting
Lasso Regression
Lasso regression is a sort of regularization method that provides a penalty time period to the loss operate, forcing sure coefficients to turn into zero. This leads to a extra parsimonious mannequin that’s much less more likely to overfit the information. By lowering the variety of options, the mannequin turns into extra sturdy and simpler to interpret.
Equation: min(β^T Xy + λ ||β||1)
Ridge Regression
Ridge regression is one other kind of regularization method that provides a penalty time period to the loss operate, however not like Lasso regression, it doesn’t drive any coefficients to turn into zero. As a substitute, it shrinks all of the coefficients in the direction of zero, leading to a extra secure mannequin.
Generalized Linear Fashions: Modeling Non-Linear Relationships
Generalized linear fashions present a framework for modeling non-linear relationships between variables. By specifying the hyperlink operate, you may create a mannequin that captures the nuances of the information.
Dealing with Lacking Information: An Overview
Dealing with lacking knowledge is a essential facet of regression evaluation. When confronted with lacking values, you have got a number of choices: listwise deletion, imputation, and a number of imputation.
Wrap-Up: Which Regression Equation Finest Suits The Information

In conclusion, deciding on the right regression equation is a essential step in regression evaluation. By understanding the various kinds of regression equations and how one can apply them, researchers and analysts can acquire correct outcomes and make knowledgeable selections. This information has supplied a complete overview of the completely different strategies for becoming knowledge, evaluating the match of a regression equation, and figuring out one of the best regression equation for a given dataset. We hope this narrative has been useful in your quest to grasp the artwork of regression evaluation.
FAQ Compilation
What’s regression evaluation?
Regression evaluation is a statistical method used to determine the connection between variables. It’s a highly effective instrument used to foretell the worth of a dependent variable based mostly on the worth of a number of impartial variables.
What are the various kinds of regression equations?
The various kinds of regression equations embrace linear regression, polynomial regression, logarithmic regression, and non-linear regression. Every kind of regression equation is used to mannequin various kinds of relationships between variables.
What’s the significance of choosing the right regression equation?
Choosing the right regression equation is essential in acquiring correct outcomes. A poor alternative can result in inaccurate predictions and flawed conclusions.
What’s the distinction between residual plots and partial regression plots?
Residual plots are used to judge the match of a regression equation, whereas partial regression plots are used to determine the connection between two variables whereas controlling for the impact of different variables.
What’s cross-validation?
Cross-validation is a method used to judge the efficiency of a regression equation by dividing the information into coaching and testing units and evaluating the mannequin on the testing set.